WHAT IS BEAM AND IT'S TYPES

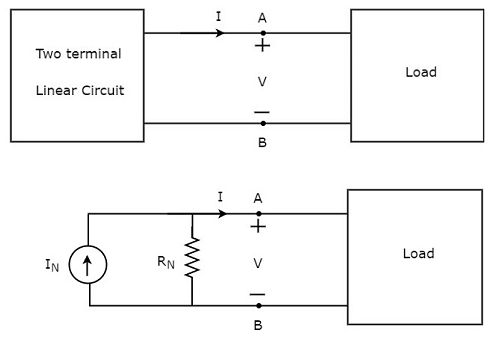
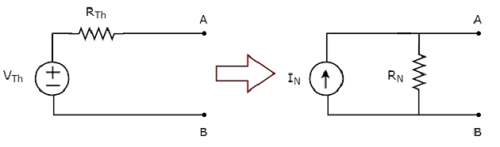
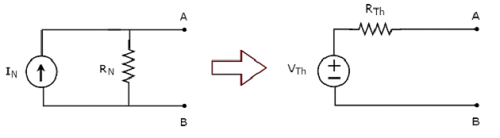
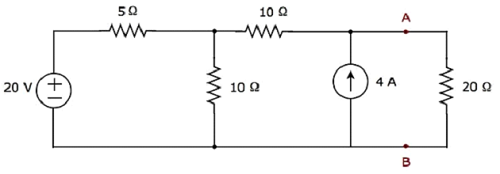
A beam is a structural member used for bearing loads. It is typically used for resisting vertical loads, shear forces and bending moments.

According to its requirement, different beams use in different conditions like fix beam, cantilever beam etc.

Types of beams:

Beams are classified as follow.

According to end support:

1. Simply Supported Beam:

As the name implies, simply supported beam is supported at both end. One end of the beam is supported by hinge support and other one by roller support. This support allow to horizontal movement of beam. It beam type undergoes both shear stress and bending moment.

2. Continuous Beams:

When we talk about types of beams we cannot forgot continuous beam. This beam is similar to simply supported beam except more than two support are used on it. One end of it is supported by hinged support and other one is roller support. One or more supports are use between these beams. It is used in long concrete bridges where length of bridge is too large.

3. Overhanging Beams:

Overhanging beam is combination of simply supported beam and cantilever beam. One or both of end overhang of this beam. This beam is supported by roller support between two ends. This type of beam has heritage properties of cantilever and simply supported beam.

4. Cantilever Beams:

Cantilever beams a structure member of which one end is fixed and other is free. This is one of the famous type of beam use in trusses, bridges and other structure member. This beam carry load over the span which undergoes both shear stress and bending moment.

5. Fixed beams:

This beam is fixed from both ends. It does not allow vertical movement and rotation of the beam. It is only under shear stress and no moment produces in this beams. It is used in trusses, and other structure.

According to cross section:

A beam may have different cross section. The most common cross section of beam are as follow.

1. I beam:

This beam types have I cross section as shown in figure. It has high resistance of bending.

2. T beam:

It has T cross section as shown in figure.

According to equilibrium condition:

1. Statically determinate beam:

A beam is called determinate beam if it can be analyze by the basic equilibrium condition. The support reaction can be found by using basic equilibrium condition. These conditions are

Summation of all horizontal forces is zero.

Summation of all vertical forces is zero.

Summation of all moments is zero.

Example: Simply supported beam, Cantilever beam etc.

2. Statically indeterminate beam:

If the beam cannot be analysis by using basic equilibrium condition, known as statically indeterminate beam. The end reaction find out by using basic equilibrium condition with combination of other conditions like strain energy method, virtual work method etc.

Example: Continuous beam, fixed beam

According to Geometry:

1. Straight beam

2. Curved beam

3. Tapper beam.

NORTON'S THEOREM

Norton’s theorem is similar to Thevenin’s theorem. It states that any two terminal linear network or circuit can be represented with an equivalent network or circuit, which consists of a current source in parallel with a resistor. It is known as Norton’s equivalent circuit. A linear circuit may contain independent sources, dependent sources and resistors.

If a circuit has multiple independent sources, dependent sources, and resistors, then the response in an element can be easily found by replacing the entire network to the left of that element with a Norton’s equivalent circuit.

The response in an element can be the voltage across that element, current flowing through that element or power dissipated across that element.

This concept is illustrated in following figures.

Norton’s equivalent circuit resembles a practical current source. Hence, it is having a current source in parallel with a resistor.

• The current source present in the Norton’s equivalent circuit is called as Norton’s equivalent current or simply Norton’s current IN.
• The resistor present in the Norton’s equivalent circuit is called as Norton’s equivalent resistor or simply Norton’s resistor RN.

Methods of Finding Norton’s Equivalent Circuit

There are three methods for finding a Norton’s equivalent circuit. Based on the type of sources that are present in the network, we can choose one of these three methods. Now, let us discuss these three methods one by one.

Method 1

Follow these steps in order to find the Norton’s equivalent circuit, when only the sources of independent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which, the Norton’s equivalent circuit is to be found.
• Step 2 − Find the Norton’s current IN by shorting the two opened terminals of the above circuit.
• Step 3 − Find the Norton’s resistance RN across the open terminals of the circuit considered in Step1 by eliminating the independent sources present in it. Norton’s resistance RN will be same as that of Thevenin’s resistance RTh.
• Step 4 − Draw the Norton’s equivalent circuit by connecting a Norton’s current IN in parallel with Norton’s resistance RN.

Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.

Method 2

Follow these steps in order to find the Norton’s equivalent circuit, when the sources of both independent type and dependent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which the Norton’s equivalent circuit is to be found.
• Step 2 − Find the open circuit voltage VOC across the open terminals of the above circuit.
• Step 3 − Find the Norton’s current IN by shorting the two opened terminals of the above circuit.
• Step 4 − Find Norton’s resistance RN by using the following formula.

RN=VOCIN$$R_N=\frac{V_{OC}}{I_N}$$

• Step 5 − Draw the Norton’s equivalent circuit by connecting a Norton’s current IN in parallel with Norton’s resistance RN.

Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.

Method 3

This is an alternate method for finding a Norton’s equivalent circuit.

• Step 1 − Find a Thevenin’s equivalent circuit between the desired two terminals. We know that it consists of a Thevenin’s voltage source, VTh and Thevenin’s resistor, RTh.
• Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. We will get the Norton’s equivalent circuit. Here,

Norton’s current,

IN=VThRTh$$I_N=\frac{V_{Th}}{R_{Th}}$$

Norton’s resistance,

RN=RTh$$R_N=R_{Th}$$

This concept is illustrated in the following figure.

Now, we can find the response in an element by placing Norton’s equivalent circuit to the left of that element.

Note − Similarly, we can find the Thevenin’s equivalent circuit by finding a Norton’s equivalent circuit first and then apply source transformation technique to it. This concept is illustrated in the following figure.

This is the Method 3 for finding a Thevenin’s equivalent circuit.

Example

Find the current flowing through 20 Ω resistor by first finding a Norton’s equivalent circuit to the left of terminals A and B.

Let us solve this problem using Method 3.

Step 1 − In previous chapter, we calculated the Thevenin’s equivalent circuit to the left side of terminals A & B. We can use this circuit now. It is shown in the following figure.

Here, Thevenin’s voltage, VTh=2003V$V_{Th}=\frac{200}{3}V$ and Thevenin’s resistance, RTh=403Ω$R_{Th}=\frac{40}{3}\mathrm{\Omega }$

Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. Substitute the values of VTh and RTh in the following formula of Norton’s current.

IN=VThRTh$$I_N=\frac{V_{Th}}{R_{Th}}$$

IN=2003403=5A$$I_N=\frac{\frac{200}{3}}{\frac{40}{3}}=5A$$

Therefore, Norton’s current IN is 5 A.

We know that Norton’s resistance, RN is same as that of Thevenin’s resistance RTh.

RN=403Ω$${\mathbf{R}}_{\mathbf{N}}\mathbf{=}\frac{\mathbf{40}}{\mathbf{3}}\mathbf{\Omega }$$

The Norton’s equivalent circuit corresponding to the above Thevenin’s equivalent circuit is shown in the following figure.

Now, place the Norton’s equivalent circuit to the left of the terminals A & B of the given circuit.

By using current division principle, the current flowing through the 20 Ω resistor will be

I20Ω=5⟮403403+20⟯$$I_{20\mathrm{\Omega }}=5⟮\frac{\frac{40}{3}}{\frac{40}{3}+20}⟯$$

I20Ω=5⟮40100⟯=2A$$I_{20\mathrm{\Omega }}=5⟮\frac{40}{100}⟯=2A$$

Therefore, the current flowing through the 20 Ω resistor is 2 A.